Zero knowledge proofs and nano nodes

Looking back, nano syncing in Nimiq 1.0 worked by leveraging two technologies: light clients and NiPoPoWs. How is that going to work in Nimiq 2.0 with Proof-of-Stake? Let’s get into the technical details with this blog post series.

One of the big strengths of Nimiq are the nano nodes and how they allow anyone to sync and connect to the blockchain from a regular phone in just a few seconds. They enable us to deliver Nimiq’s vision of making crypto accessible to the masses.

Light clients are ubiquitous in crypto and simply refer to nodes that only download the headers of the block and ignore both the transactions and the state. This evidently greatly reduces the amount of data that a user needs to download, but it still is too much for a browser or a mobile. Even Bitcoin, with its small block headers and very large block time, requires its light clients to download roughly 50 MB to sync from the genesis block. And that number is growing at a steady 4 MB per year. Calculating these numbers is simple as Bitcoin block headers are always 80 bytes. For Nimiq, with a blocktime of one minute and a header of 146 bytes, the size would be almost twenty-fold. That is not light at all 😉.

NiPoPoWs, or Non-Interactive Proofs of Proof-of-Work, are short proofs that can prove that a given amount of computational power was spent in producing a chain of blocks, without the need of taking all block headers into account. In essence, it allows a light client to sync the blockchain while downloading only a small fraction of all the block headers. Without getting too technical, it does this by identifying blocks that greatly exceed their difficulty target, which happens now and then. If you want to read more on the topic, check out nipopows.com or the Nimiq 1.0 whitepaper.

However, now that Nimiq is transitioning to a Proof-of-Stake-based protocol, we can no longer use NiPoPoWs, since they are specific to Proof-of-Work. So, we started to work on a novel solution to deliver Nimiq’s vision of being browser-first.

It turned out, developing nano nodes for a PoS blockchain is an interesting challenge as the blockchain research community is just starting to work on this field. Thanks to the efforts of the team’s researchers, Bruno and Pascal, and their longstanding experience in scientific and blockchain research, a solution using zero knowledge proofs has been found! With this post we will explain, in some technical detail, what were the issues we faced and how we found an optimal solution. If you want to meet Bruno and Pascal, check out this video where they explain Nimiq 2.0 tech.

Warning, technical content ahead! 🤓

To get the best out of this post, you should have a basic understanding of what elliptic curves, zero knowledge proofs — or ZKPs for short — and SNARKs are. And here are some resources for those interested in diving deeper:

• The best site for ZKPs is zkp.science. It's a collection of resources about ZKPs.
• Also, this GitHub repo has some great links to further reading
• Or read Vitalik’s famous three post series on ZKPs: First, second, third.

Albatross, the new consensus algorithm in Nimiq 2.0, will have a block time on the order of one second. That means, while Bitcoin produces 52’560 blocks per year, Nimiq 2.0 will produce 86’400 blocks per day! While this performance improvement is incredible, with so many blocks being produced, syncing the blockchain becomes a new unexpected challenge.

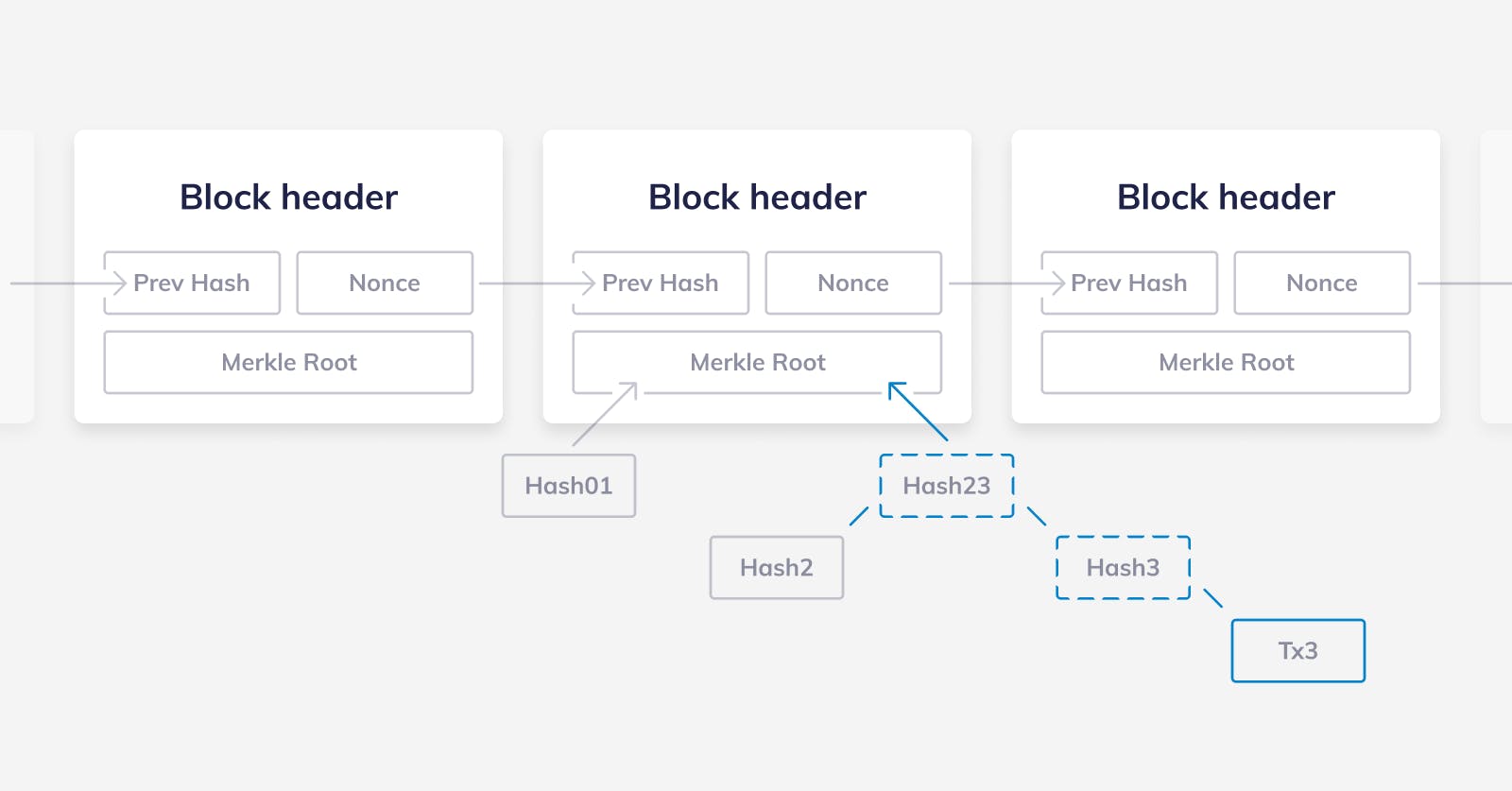
Now, let’s have a look at how a light client works in Albatross. A regular light client in other blockchains forces the user to download all of the block headers from genesis to the current time. This is necessary in order to find out what the most recent block is. Next, the user can request Merkle proofs to whatever part she is interested in. Merkle proofs allow a light client to verify that a given transaction, or account, is part of a block without needing to download the entire block. 

Albatross, like many other PoS algorithms, picks a random set of nodes to be validators — called the validator set — and lets them produce a fixed number of blocks — which is called an epoch. At the end of an epoch, a new set of nodes will be randomly picked.

In Albatross, macro blocks mark the end of an epoch and the beginning of another one, it’s where the validator set changes. Between any two macro blocks, the validator set doesn’t change, that means that we can safely skip all of the micro blocks between two macro blocks.

So, a light client in Albatross would download only the macro block headers since genesis to the most recent one and all of the micro block headers produced in the current epoch. Then, once again, the user can ask for Merkle proofs for parts of the state.

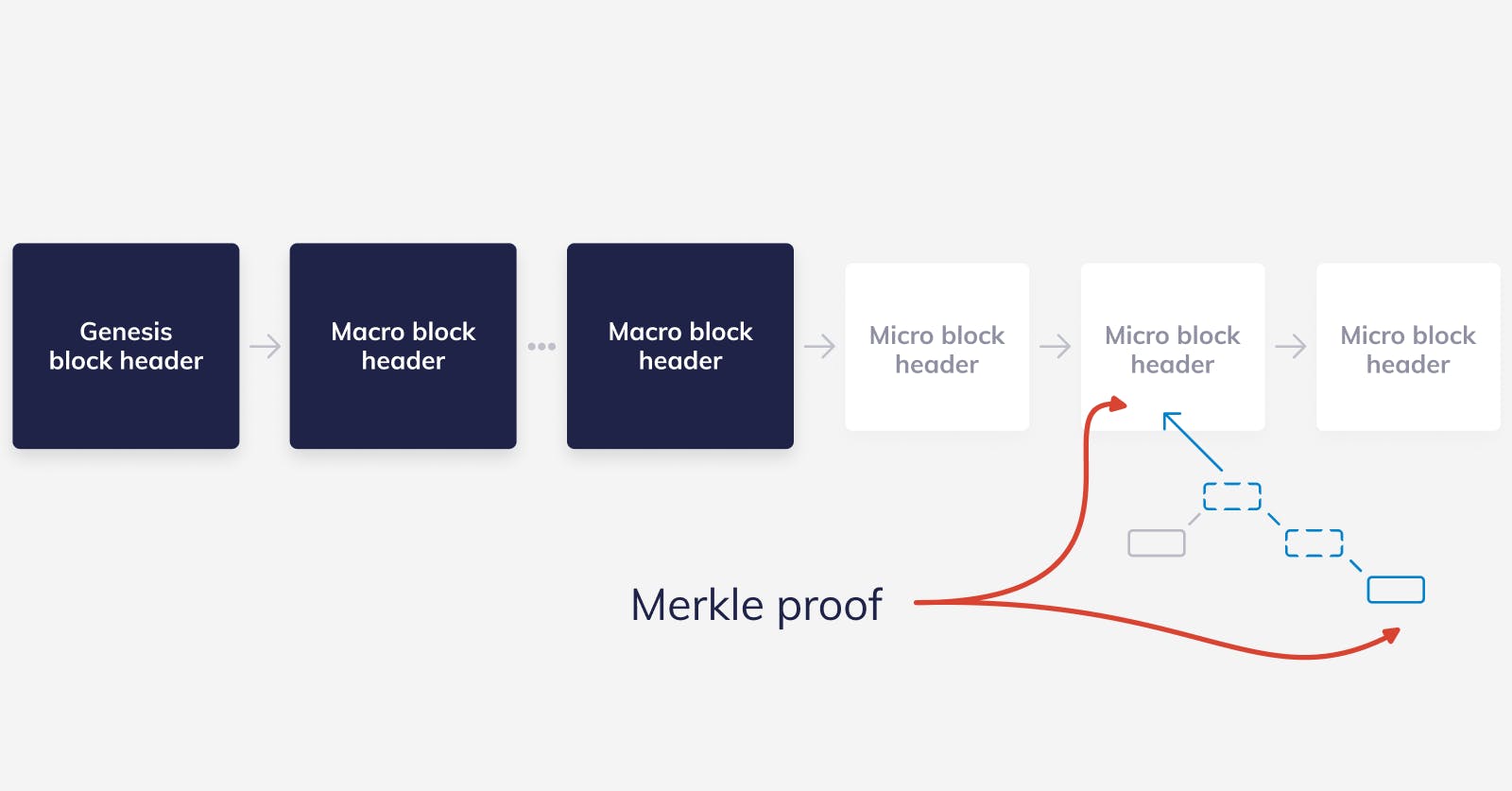
Skipping the micro blocks is already a huge improvement. Macro blocks might only happen once per day — the exact frequency is still to be decided — while micro blocks happen tens of thousands of times per day.

Let’s do some math. Considering that a block header for a PoS chain needs to include the public keys of each validator and assuming 1024 validators per epoch, that will give us 290kB for the public keys only. Then, a quick calculation — assuming a macro block header of 300kB and one macro block being produced per day — shows us that the required download would grow to 109MB within just one year. That is too much for a web and mobile environment! This got us on the journey of finding a better solution: Zero knowledge proofs, more specifically zk-SNARKs!

Zk-SNARKs, or Zero-Knowledge Succinct Non-Interactive Argument of Knowledge, are probably the most famous type of zero knowledge proofs and have found a lot of use cases in blockchain recently. As a zero knowledge proof, they are known for their ability to prove arbitrary statements without revealing any other information other than that the statement is true. This property is leveraged by Zcash, which is also arguably the first blockchain to make extensive use of zero knowledge proofs. However, we are not interested in the zero knowledge property of SNARKs but rather on its succinctness. 

Succinctness refers to the ability of SNARKs to take a statement of any size and prove its correctness with a very small proof that is very quick to verify. A statement in this case can be a simple calculation or an entire program that returns true or false. So, in other words, this allows us to do some large calculation and then produce a proof that the calculation was performed correctly. Then, anyone can simply check the proof instead of redoing the same calculation. SNARKs are exceptionally succinct, producing proofs with sizes of a few hundreds bytes that take only milliseconds to verify. If you want to dive deeper, consider reading this article.

Normally, a light client needs to download all of the macro block headers to verify that the last macro block header it received is indeed authentic. All of those intermediate macro block headers are just a way of getting from the genesis macro block to the most recent macro block. So here lies the optimal solution: Using the succinctness of SNARKs to compress all that computation into a small proof!

That leads us to nano nodes. While light nodes need to download all of the macro block headers, nano nodes only ask for the most recent one and a SNARK attesting to the fact that there is a valid chain of macro block headers that start with the genesis block and end in the most recent block. Note, we can assume that it has the genesis macro block header already as it is public knowledge. The SNARK is enough for the node to be convinced that the macro block header that it received is valid. After that, it just needs to download the headers of the micro blocks in the current epoch plus whatever Merkle proofs it needs.

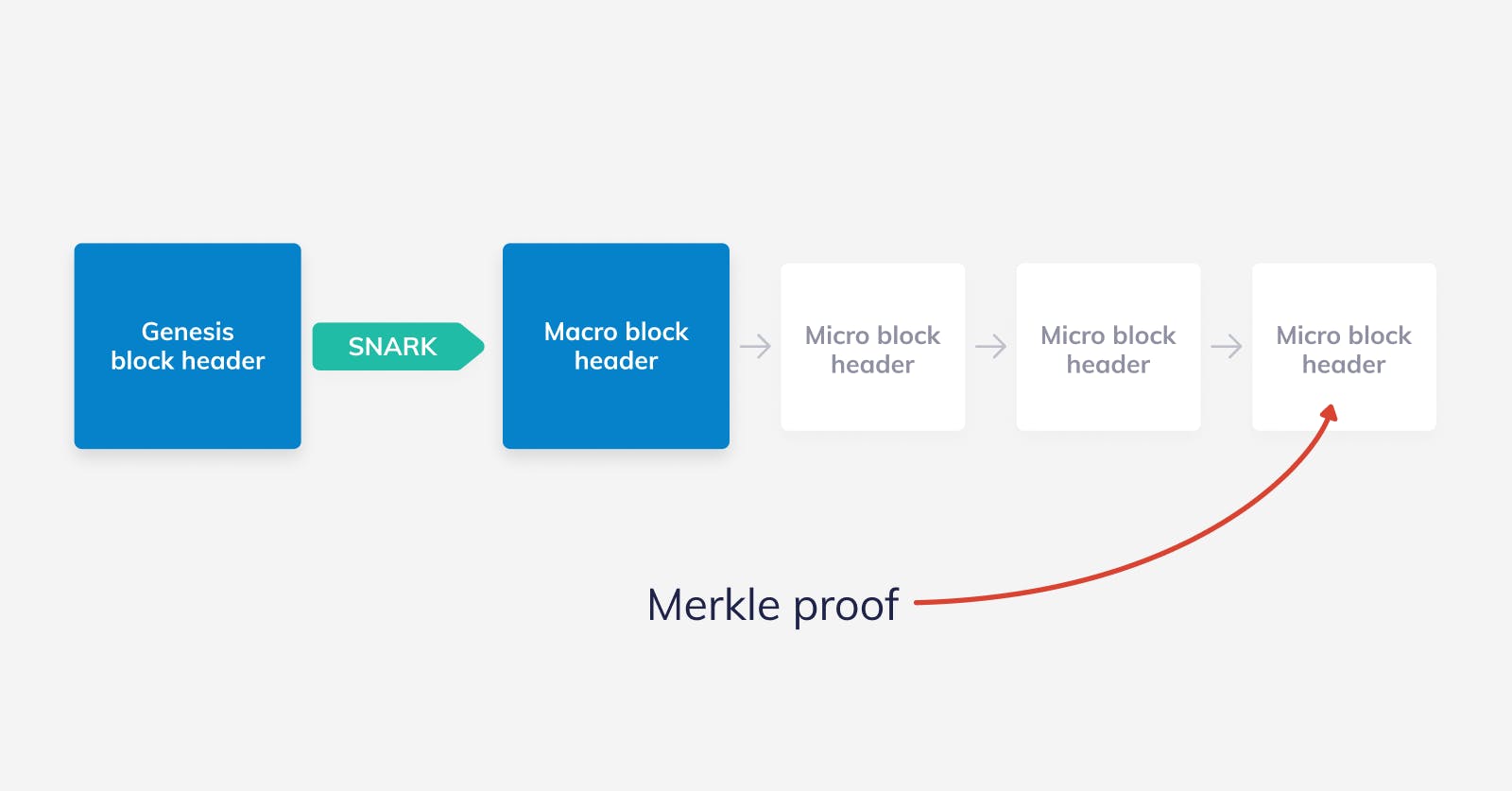
This ideal solution would mean that a user can sync with the blockchain in a few seconds maximum. The data that needs to be downloaded would include the last macro block header of ~300kB, tiny 200 bytes for the SNARK, about 400 bytes for each micro block headers in the current epoch and ~200 bytes for all the necessary Merkle proofs. So, in total, we're talking about ~400-500 kB to sync. That is completely doable in a mobile/browser environment!

But the best part is that the syncing time will never increase! Indeed, it’s a fixed size, no matter how large the Nimiq blockchain grows, it will stay the same!

However, while verifying SNARKS is very quick, creating them is a big effort. So, while it’s theoretically possible to create one new SNARK verifying the entire chain of macro blocks at the end of each epoch, it would put a big burden on the validator.

Instead, we are using a strategy where our SNARK proof will be extended with each new macro block without growing the size of the proof. We can do this by using a very recent, very promising technique called “recursive SNARKs”.

This has been a long and technical post, thanks for coming with us on this journey. Let’s take a break and explore the specifics on how to achieve this in part 2 of this series.

Pura vida,

Team Nimiq